|
|
|
The first Smarandache constant is defined as
![\begin{displaymath}
S_1\equiv \sum_{n=2}^\infty {1\over [S(n)]!} > 1.093111,
\end{displaymath}](s2_167.gif)
Cojocaru and Cojocaru (1996b) prove that the second Smarandache constant
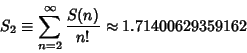
Cojocaru and Cojocaru (1996c) prove that the series
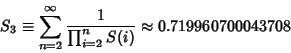
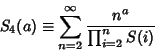
Sandor (1997) shows that the series
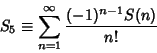
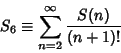
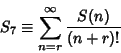
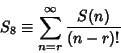
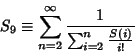
![\begin{displaymath}
S_{10}\equiv\sum_{n=2}^\infty {1\over [S(n)]^\alpha\sqrt{S(n)!}}
\end{displaymath}](s2_193.gif)
![\begin{displaymath}
S_{11}\equiv\sum_{n=2}^\infty {1\over [S(n)]^\alpha\sqrt{[S(n)+1]!}}
\end{displaymath}](s2_194.gif)
See also Smarandache Function
References
Burton, E. ``On Some Series Involving the Smarandache Function.'' Smarandache Notions J. 6, 13-15, 1995.
Burton, E. ``On Some Convergent Series.'' Smarandache Notions J. 7, 7-9, 1996.
Cojocaru, I. and Cojocaru, S. ``The First Constant of Smarandache.'' Smarandache Notions J. 7, 116-118, 1996a.
Cojocaru, I. and Cojocaru, S. ``The Second Constant of Smarandache.'' Smarandache Notions J. 7, 119-120, 1996b.
Cojocaru, I. and Cojocaru, S. ``The Third and Fourth Constants of Smarandache.'' Smarandache Notions J. 7, 121-126, 1996c.
``Constants Involving the Smarandache Function.''
http://www.gallup.unm.edu/~smarandache/CONSTANT.TXT.
Dumitrescu, C. and Seleacu, V. ``Numerical Series Involving the Function
Ibstedt, H. Surfing on the Ocean of Numbers--A Few Smarandache Notions and Similar Topics.
Lupton, AZ: Erhus University Press, pp. 27-30, 1997.
Sandor, J. `On The Irrationality Of Certain Alternative Smarandache Series.'' Smarandache Notions J. 8, 143-144, 1997.
Smarandache, F. Collected Papers, Vol. 1. Bucharest, Romania: Tempus, 1996.
Smarandache, F. Collected Papers, Vol. 2. Kishinev, Moldova: Kishinev University Press, 1997.
![]() .'' The Smarandache Function.
Vail: Erhus University Press, pp. 48-61, 1996.
.'' The Smarandache Function.
Vail: Erhus University Press, pp. 48-61, 1996.
|
|
|
© 1996-9 Eric W. Weisstein