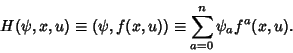A result is Control Theory. Define
Then in order for a control 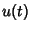 and a trajectory
and a trajectory 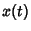 to be optimal, it is Necessary that there exist
Nonzero absolutely continuous vector function
to be optimal, it is Necessary that there exist
Nonzero absolutely continuous vector function
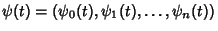 corresponding to
the functions
corresponding to
the functions 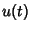 and
and 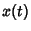 such that
such that
- 1. The function
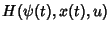 attains its maximum at the point
attains its maximum at the point 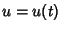 almost everywhere in the interval
almost everywhere in the interval
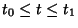 ,
,
- 2. At the terminal time
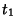 , the relations
, the relations
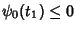 and
and
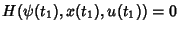 are
satisfied.
are
satisfied.
References
Iyanaga, S. and Kawada, Y. (Eds.). ``Pontrjagin's [sic] Maximum Principle.'' §88C in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 295-296, 1980.
© 1996-9 Eric W. Weisstein
1999-05-26