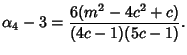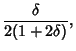Generalizes the differential equation for the Gaussian Distribution
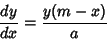 |
(1) |
to
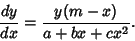 |
(2) |
Let 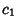 ,
, 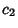 be the roots of
be the roots of 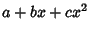 . Then the possible types of curves are
. Then the possible types of curves are
- 0.
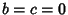 ,
, 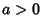 . E.g., Normal Distribution.
. E.g., Normal Distribution.
- I.
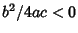 ,
,
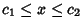 . E.g., Beta Distribution.
. E.g., Beta Distribution.
- II.
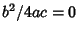 ,
, 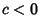 ,
,
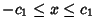 where
where
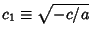 .
.
- III.
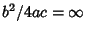 ,
, 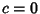 ,
,
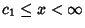 where
where
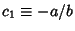 . E.g., Gamma Distribution. This case is
intermediate to cases I and VI.
. E.g., Gamma Distribution. This case is
intermediate to cases I and VI.
- IV.
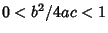 ,
,
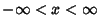 .
.
- V.
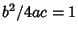 ,
,
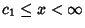 where
where
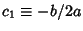 . Intermediate to cases IV and VI.
. Intermediate to cases IV and VI.
- VI.
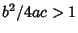 ,
,
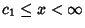 where
where 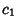 is the larger root. E.g., Beta Prime Distribution.
is the larger root. E.g., Beta Prime Distribution.
- VII.
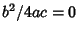 ,
, 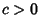 ,
,
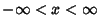 . E.g., Student's t-Distribution.
. E.g., Student's t-Distribution.
Classes IX-XII are discussed in Pearson (1916). See also Craig (in Kenney and Keeping 1951). If a Pearson curve possesses a
Mode, it will be at 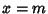 . Let
. Let 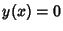 at
at 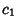 and
and 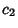 , where these may be
, where these may be 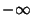 or
or 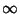 . If
. If
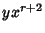 also vanishes at
also vanishes at 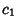 ,
, 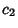 , then the
, then the 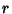 th Moment and
th Moment and 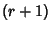 th Moments exist.
th Moments exist.
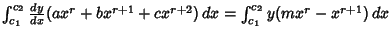
|
|
|
|
(3) |
giving
![$[y(ax^r+bx^{r+1}+cx^{r+2})]_{c_1}^{c_2}-\int_{c_1}^{c_2} y[arx^{r-1}+b(r+1)x^r+c(r+2)x^{r+1}]\,dx$](p1_922.gif)
|
|
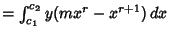
|
(4) |
![\begin{displaymath}
0-\int_{c_1}^{c_2} y[arx^{r-1}+b(r+1)x^r+c(r+2)x^{r+1}]\,dx = \int_{c_1}^{c_2} y(mx^r-x^{r+1})\,dx
\end{displaymath}](p1_924.gif) |
(5) |
also,
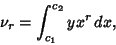 |
(6) |
so
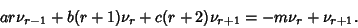 |
(7) |
For 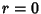 ,
,
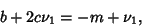 |
(8) |
so
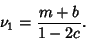 |
(9) |
For 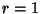 ,
,
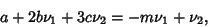 |
(10) |
so
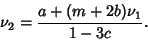 |
(11) |
Now let
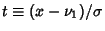 . Then
. Then
Hence 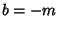 , and
, and 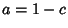 so
so
![\begin{displaymath}
(1-3c)r\alpha_{r-1}-mr\alpha_r+[c(r+2)-1]\alpha_{r+1}=0.
\end{displaymath}](p1_941.gif) |
(15) |
For 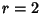 ,
,
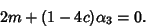 |
(16) |
For 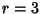 ,
,
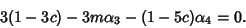 |
(17) |
So the Skewness and Kurtosis are
So the parameters 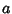 ,
, 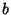 , and
, and 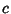 can be written
can be written
where
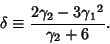 |
(23) |
References
Craig, C. C. ``A New Exposition and Chart for the Pearson System of Frequency Curves.'' Ann. Math. Stat. 7, 16-28, 1936.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, p. 107, 1951.
Pearson, K. ``Second Supplement to a Memoir on Skew Variation.'' Phil. Trans. A 216, 429-457, 1916.
© 1996-9 Eric W. Weisstein
1999-05-26