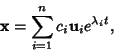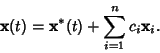To solve the system of differential equations
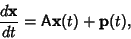 |
(1) |
where
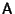 is a Matrix and
is a Matrix and 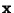 and
and 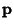 are Vectors, first consider the homogeneous
case with
are Vectors, first consider the homogeneous
case with
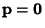 . Then the solutions to
. Then the solutions to
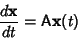 |
(2) |
are given by
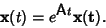 |
(3) |
But, by the Matrix Decomposition Theorem, the Matrix Exponential can be written as
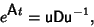 |
(4) |
where the Eigenvector Matrix is
![\begin{displaymath}
{\hbox{\sf u}} = \left[{\matrix{{\bf u}_1 & \cdots & {\bf u}_n\cr}}\right]
\end{displaymath}](o_804.gif) |
(5) |
and the Eigenvalue Matrix is
![\begin{displaymath}
{\hbox{\sf D}} = \left[{\matrix{e^{\lambda_1t} & 0 &\cdots &...
... & \ddots & 0\cr
0 & 0 & \cdots & e^{\lambda_nt}\cr}}\right].
\end{displaymath}](o_805.gif) |
(6) |
Now consider
The individual solutions are then
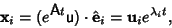 |
(8) |
so the homogeneous solution is
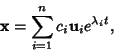 |
(9) |
where the 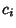 s are arbitrary constants.
s are arbitrary constants.
The general procedure is therefore
- 1. Find the Eigenvalues of the Matrix
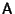 (
(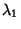 , ...,
, ..., 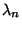 ) by
solving the Characteristic Equation.
) by
solving the Characteristic Equation.
- 2. Determine the corresponding Eigenvectors
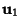 , ...,
, ..., 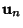 .
.
- 3. Compute
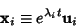 |
(10) |
for 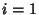 , ...,
, ..., 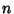 . Then the Vectors
. Then the Vectors 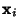 which are Real are
solutions to the homogeneous equation. If
which are Real are
solutions to the homogeneous equation. If
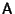 is a
is a 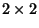 matrix, the Complex vectors
matrix, the Complex vectors
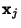 correspond to Real solutions to the homogeneous equation given by
correspond to Real solutions to the homogeneous equation given by
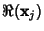 and
and
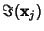 .
.
- 4. If the equation is nonhomogeneous, find the particular solution given by
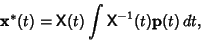 |
(11) |
where the Matrix
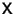 is defined by
is defined by
![\begin{displaymath}
{\hbox{\sf X}}(t) \equiv \left[{\matrix{{\bf x}_1 & \cdots & {\bf x}_n\cr}}\right].
\end{displaymath}](o_825.gif) |
(12) |
If the equation is homogeneous so that
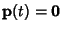 , then look for a solution of the form
, then look for a solution of the form
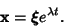 |
(13) |
This leads to an equation
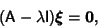 |
(14) |
so 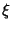 is an Eigenvector and
is an Eigenvector and 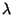 an Eigenvalue.
an Eigenvalue.
- 5. The general solution is
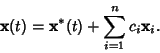 |
(15) |
© 1996-9 Eric W. Weisstein
1999-05-26
![\begin{displaymath}
{\hbox{\sf D}} = \left[{\matrix{e^{\lambda_1t} & 0 &\cdots &...
... & \ddots & 0\cr
0 & 0 & \cdots & e^{\lambda_nt}\cr}}\right].
\end{displaymath}](o_805.gif)
![$\displaystyle \left[\begin{array}{cccc} u_{11} & u_{21} & \cdots & u_{n1}\\ u_...
...dots & \vdots & \ddots & 0\\ 0 & 0 & \cdots & e^{\lambda_nt}\end{array}\right]$](o_808.gif)
![$\displaystyle \left[\begin{array}{ccc} u_{11}e^{\lambda_1t} & \cdots & u_{n1}e^...
...dots\\ u_{n1}e^{\lambda_1t} & \cdots & u_{n2}e^{\lambda_nt}\end{array}\right].$](o_809.gif)