|
|
|
A ![]() -multigrade equation is a Diophantine Equation of the form
-multigrade equation is a Diophantine Equation of the form
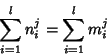
Small-order examples are the (2, 3)-multigrade with
![]() and
and
![]() :
:
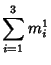 |
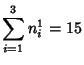 |
||
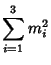 |
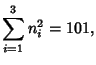 |
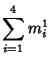 |
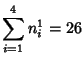 |
||
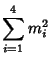 |
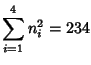 |
||
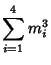 |
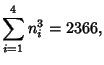 |
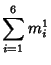 |
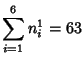 |
||
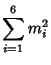 |
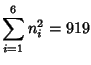 |
||
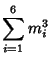 |
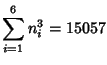 |
||
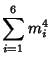 |
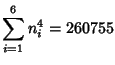 |
A spectacular example with ![]() and
and ![]() is given by
is given by
![]() and
and
![]() (Guy 1994), which has sums
(Guy 1994), which has sums
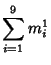 |
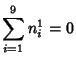 |
||
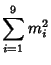 |
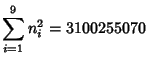 |
||
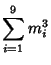 |
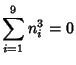 |
||
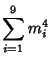 |
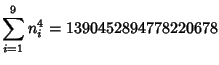 |
||
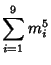 |
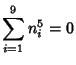 |
||
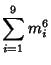 |
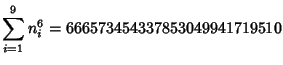 |
||
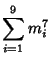 |
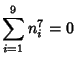 |
||
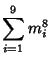 |
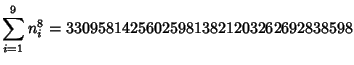 |
||
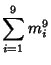 |
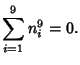 |
See also Diophantine Equation
References
Chen, S. ``Equal Sums of Like Powers: On the Integer Solution of the Diophantine System.''
http://www.nease.net/~chin/eslp/
Gloden, A. Mehrgeradige Gleichungen. Groningen, Netherlands: Noordhoff, 1944.
Gloden, A. ``Sur la multigrade
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 143, 1994.
Kraitchik, M. ``Multigrade.'' §3.10 in Mathematical Recreations. New York: W. W. Norton, p. 79, 1942.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, pp. 171-173, 1979.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (
(![]() , 3, 5, 7).''
Revista Euclides 8, 383-384, 1948.
, 3, 5, 7).''
Revista Euclides 8, 383-384, 1948.
|
|
|
© 1996-9 Eric W. Weisstein