|
|
|
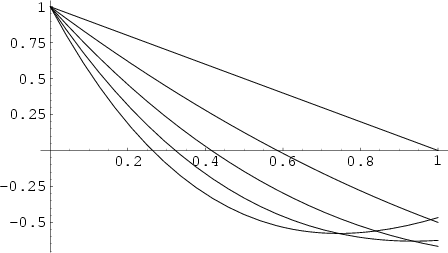
Solutions to the Laguerre Differential Equation with ![]() are called Laguerre polynomials. The Laguerre
polynomials
are called Laguerre polynomials. The Laguerre
polynomials ![]() are illustrated above for
are illustrated above for ![]() and
and ![]() , 2, ..., 5.
, 2, ..., 5.
The Rodrigues formula for the Laguerre polynomials is
| (1) |
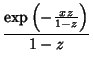 |
|||
| (2) |
| (3) |
| (4) |
| (5) |
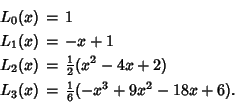
Solutions to the associated Laguerre Differential Equation with ![]() are called associated Laguerre
polynomials
are called associated Laguerre
polynomials ![]() . In terms of the normal Laguerre polynomials,
. In terms of the normal Laguerre polynomials,
| (6) |
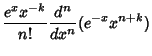 |
|||
![$\displaystyle (-1)^n {d^n\over dx^n}[L_{n+k}(x)]$](l1_260.gif) |
(7) | ||
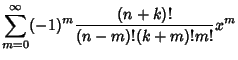 |
(8) |
![\begin{displaymath}
g(x,z)={\mathop{\rm exp}\nolimits \left({-{xz\over 1-z}}\rig...
...-x)z+{\textstyle{1\over 2}}[x^2-2(k+2)x+(k+1)(k+2)]z^2+\ldots.
\end{displaymath}](l1_262.gif) |
(9) |
| (10) |
| (11) |
Recurrence Relations include
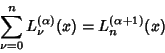 |
(12) |
| (13) |
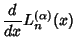 |
|||
| (14) |
In terms of the Confluent Hypergeometric Function,
| (15) |
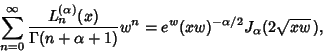 |
(16) |
| (17) |
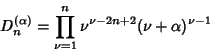 |
(18) |
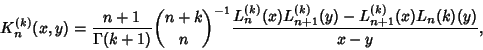 |
(19) |
The first few associated Laguerre polynomials are
![\begin{eqnarray*}
L_0^k(x) &=& 1\\
L_1^k(x) &=& -x+k+1\\
L_2^k(x) &=& {\tex...
...xtstyle{1\over 6}}[-x^3+3(k+3)x^2-3(k+2)(k+3)x+(k+1)(k+2)(k+3)].
\end{eqnarray*}](l1_281.gif)
See also Sonine Polynomial
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. ``Laguerre Functions.'' §13.2 in Mathematical Methods for Physicists, 3rd ed.
Orlando, FL: Academic Press, pp. 721-731, 1985.
Chebyshev, P. L. ``Sur le développement des fonctions à une seule variable.'' Bull. Ph.-Math.,
Acad. Imp. Sc. St. Pétersbourg 1, 193-200, 1859.
Chebyshev, P. L. Oeuvres, Vol. 1. New York: Chelsea, pp. 499-508, 1987.
Iyanaga, S. and Kawada, Y. (Eds.). ``Laguerre Functions.'' Appendix A, Table 20.VI in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, p. 1481, 1980.
Laguerre, E. de. ``Sur l'intégrale
Petkovsek, M.; Wilf, H. S.; and Zeilberger, D. A=B. Wellesley, MA: A. K. Peters, pp. 61-62, 1996.
Sansone, G. ``Expansions in Laguerre and Hermite Series.'' Ch. 4 in Orthogonal Functions, rev. English ed.
New York: Dover, pp. 295-385, 1991.
Spanier, J. and Oldham, K. B. ``The Laguerre Polynomials
Szegö, G. Orthogonal Polynomials, 4th ed. Providence, RI: Amer. Math. Soc., 1975.
![]() .'' Bull. Soc. math. France 7, 72-81, 1879.
Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971.
.'' Bull. Soc. math. France 7, 72-81, 1879.
Reprinted in Oeuvres, Vol. 1. New York: Chelsea, pp. 428-437, 1971.
![]() .''
Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987.
.''
Ch. 23 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 209-216, 1987.
|
|
|
© 1996-9 Eric W. Weisstein