Icosahedron Stellations

Applying the Stellation process to the Icosahedron gives

$\begin{displaymath} 20+30+60+20+60+120+12+30+60+60 \end{displaymath}$

cells of ten different shapes and sizes in addition to the Icosahedron itself. After application of five restrictions due to J. C. P. Miller to define which forms should be considered distinct, 59 stellations are found to be possible. Miller's restrictions are

: 1. The faces must lie in the twenty bounding planes of the icosahedron.
: 2. The parts of the faces in the twenty planes must be congruent, but those parts lying in one place may be disconnected.
: 3. The parts lying in one plane must have threefold rotational symmetry with or without reflections.
: 4. All parts must be accessible, i.e., lie on the outside of the solid.
: 5. Compounds are excluded that can be divided into two sets, each of which has the full symmetry of the whole.

Of these, 32 have full icosahedral symmetry and 27 are Enantiomeric forms. Four are Polyhedron Compounds, one is a Kepler-Poinsot Solid, and one is the Dual Polyhedron of an Archimedean Solid. The only Stellations of Platonic Solids which are Uniform Polyhedra are the three Dodecahedron Stellations the Great Icosahedron (stellation # 11).

	name
1	Icosahedron
2	Triakis Icosahedron
3	Octahedron 5-Compound
4	Echidnahedron
11	Great Icosahedron
18	Tetrahedron 10-Compound
20	Deltahedron-60
36	Tetrahedron 5-Compound

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos01.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos03.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 01 \hskip0.88in 02 \hskip0.88in 03\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos04.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos06.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 04 \hskip0.88in 05 \hskip0.88in 06\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos07.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos09.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 07 \hskip0.88in 08 \hskip0.88in 09\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos10.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos12.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 10 \hskip0.88in 11 \hskip0.88in 12\end{center}\end{figure}$

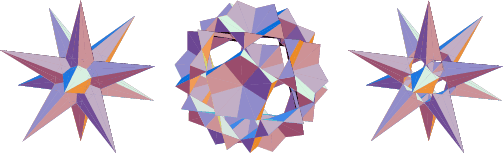
$\begin{figure}\begin{center}\BoxedEPSF{icos/icos13.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos15.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 13 \hskip0.88in 14 \hskip0.88in 15\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos16.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos18.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 16 \hskip0.88in 17 \hskip0.88in 18\end{center}\end{figure}$

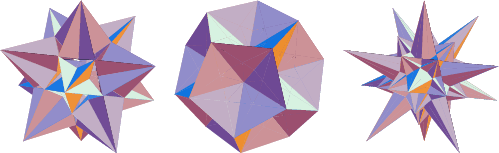
$\begin{figure}\begin{center}\BoxedEPSF{icos/icos19.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos21.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 19 \hskip0.88in 20 \hskip0.88in 21\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos22.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos24.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 22 \hskip0.88in 23 \hskip0.88in 24\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos25.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos27.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 25 \hskip0.88in 26 \hskip0.88in 27\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos28.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos30.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 28 \hskip0.88in 29 \hskip0.88in 30\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos31.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos33.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 31 \hskip0.88in 32 \hskip0.88in 33\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos34.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos36.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 34 \hskip0.88in 35 \hskip0.88in 36\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos37.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos39.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 37 \hskip0.88in 38 \hskip0.88in 39\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos40.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos42.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 40 \hskip0.88in 41 \hskip0.88in 42\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos43.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos45.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 43 \hskip0.88in 44 \hskip0.88in 45\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos46.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos48.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 46 \hskip0.88in 47 \hskip0.88in 48\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos49.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos51.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 49 \hskip0.88in 50 \hskip0.88in 51\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos52.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos54.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 52 \hskip0.88in 53 \hskip0.88in 54\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos55.epsf scaled 500}\hskip0.1in \... ... 500}\hskip0.1in \BoxedEPSF{icos/icos57.epsf scaled 500}\end{center}\end{figure}$

$\begin{figure}\begin{center}\hskip0.0in 55 \hskip0.88in 56 \hskip0.88in 57\end{center}\end{figure}$

$\begin{figure}\begin{center}\BoxedEPSF{icos/icos58.epsf scaled 500}\hskip0.1in\BoxedEPSF{icos/icos59.epsf scaled 500}\end{center}\end{figure}$

References

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 146-147, 1987.

Bulatov, V. ``Stellations of Icosahedron.'' http://www.physics.orst.edu/~bulatov/polyhedra/icosahedron/.

Coxeter, H. S. M. The Fifty-Nine Icosahedra. New York: Springer-Verlag, 1982.

Hart, G. W. ``59 Stellations of the Icosahedron.'' http://www.li.net/~george/virtual-polyhedra/stellations-icosahedron-index.html.

Maeder, R. E. Icosahedra.m notebook. http://www.inf.ethz.ch/department/TI/rm/programs.html.

Maeder, R. E. ``The Stellated Icosahedra.'' Mathematica in Education 3, 1994. ftp://ftp.inf.ethz.ch/doc/papers/ti/scs/icosahedra94.ps.gz.

Maeder, R. E. ``Stellated Icosahedra.'' http://www.mathconsult.ch/showroom/icosahedra/.

Wang, P. ``Polyhedra.'' http://www.ugcs.caltech.edu/~peterw/portfolio/polyhedra/.

Wenninger, M. J. Polyhedron Models. New York: Cambridge University Press, pp. 41-65, 1989.

Wheeler, A. H. ``Certain Forms of the Icosahedron and a Method for Deriving and Designating Higher Polyhedra.'' Proc. Internat. Math. Congress 1, 701-708, 1924.