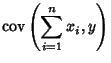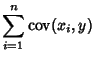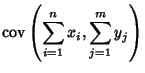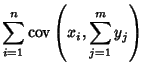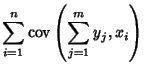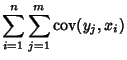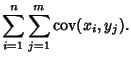Given 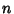 sets of variates denoted
sets of variates denoted 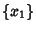 , ...,
, ..., 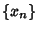 , a quantity called the Covariance Matrix is defined
by
, a quantity called the Covariance Matrix is defined
by
where
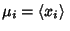 and
and
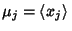 are the Means of
are the Means of 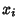 and
and 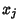 , respectively.
An individual element
, respectively.
An individual element 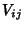 of the Covariance Matrix is called the covariance of the two variates
of the Covariance Matrix is called the covariance of the two variates 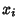 and
and
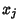 , and provides a measure of how strongly correlated these variables are. In fact, the derived quantity
, and provides a measure of how strongly correlated these variables are. In fact, the derived quantity
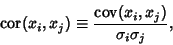 |
(4) |
where 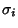 ,
, 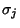 are the Standard Deviations, is called the Correlation of
are the Standard Deviations, is called the Correlation of 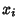 and
and 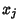 . Note that if
. Note that if 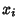 and
and 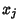 are taken from the same set of
variates (say,
are taken from the same set of
variates (say, 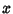 ), then
), then
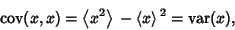 |
(5) |
giving the usual Variance
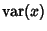 . The covariance is also symmetric since
. The covariance is also symmetric since
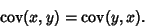 |
(6) |
For two variables, the covariance is related to the Variance by
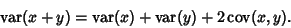 |
(7) |
For two independent variates 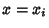 and
and 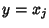 ,
,
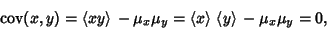 |
(8) |
so the covariance is zero. However, if the variables are correlated in some way, then their covariance will be
Nonzero. In fact, if
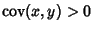 , then
, then 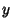 tends to increase as
tends to increase as 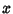 increases. If
increases. If
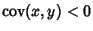 , then
, then 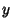 tends to decrease as
tends to decrease as 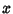 increases.
increases.
The covariance obeys the identity
By induction, it therefore follows that
See also Correlation (Statistical), Covariance Matrix, Variance
© 1996-9 Eric W. Weisstein
1999-05-25
![]() sets of variates denoted
sets of variates denoted ![]() , ...,
, ..., ![]() , a quantity called the Covariance Matrix is defined
by
, a quantity called the Covariance Matrix is defined
by
![]() and
and ![]() ,
,