|
|
|
An iterative algorithm which Deconvolves a sampling function (the ``Dirty Beam'') from an
observed brightness (``Dirty Map'') of a radio source. This algorithm is of fundamental importance in radio
astronomy, where it is used to create images of astronomical sources which are observed using arrays of radio telescopes
(``synthesis imaging ![]() ''). As a result of the algorithm's importance to
synthesis imaging
''). As a result of the algorithm's importance to
synthesis imaging ![]() , a great deal of effort has gone into optimizing and adjusting the Algorithm.
CLEAN is a nonlinear algorithm, since linear Deconvolution algorithms such as Wiener Filtering and inverse filtering are inapplicable to applications with invisible distributions (i.e., incomplete sampling of the
spatial frequency plane) such as maps obtained in synthesis imaging
, a great deal of effort has gone into optimizing and adjusting the Algorithm.
CLEAN is a nonlinear algorithm, since linear Deconvolution algorithms such as Wiener Filtering and inverse filtering are inapplicable to applications with invisible distributions (i.e., incomplete sampling of the
spatial frequency plane) such as maps obtained in synthesis imaging ![]() .
.
The basic CLEAN method was developed by Högbom (1974). It was originally designed for point sources, but it has been
found to work well for extended sources as well when given a reasonable starting model. The Högbom CLEAN constructs
discrete approximations ![]() to the CLEAN Map in the
to the CLEAN Map in the ![]() plane from the Convolution equation
plane from the Convolution equation
| (1) |
The CLEAN algorithm starts with an initial approximation ![]() . At the
. At the ![]() th iteration, it then searches for the largest
value in the residual map
th iteration, it then searches for the largest
value in the residual map
| (2) |
To diminish high spatial frequency features which may be spuriously extrapolated from the measured data, each CLEAN component
is convolved with the so-called CLEAN Beam ![]() , which is simply a suitably smoothed version of the sampling function
(``Dirty Beam''). Usually, a Gaussian is used. A good CLEAN Beam should:
, which is simply a suitably smoothed version of the sampling function
(``Dirty Beam''). Usually, a Gaussian is used. A good CLEAN Beam should:
| (3) |
CLEAN will always converge to one (of possibly many) solutions if the following three conditions are satisfied (Schwarz 1978):
These conditions are almost always satisfied in practice. If the number of CLEAN components does not exceed the number of
independent ![]() points, CLEAN converges to a solution which is the least squares fit of the Fourier
Transforms of the Delta Function components to the measured visibility (Thompson et al. 1986,
p. 347). Schwarz claims that the CLEAN algorithm is equivalent to a least squares fitting of cosine and sine parts in the
points, CLEAN converges to a solution which is the least squares fit of the Fourier
Transforms of the Delta Function components to the measured visibility (Thompson et al. 1986,
p. 347). Schwarz claims that the CLEAN algorithm is equivalent to a least squares fitting of cosine and sine parts in the
![]() plane of the visibility data. Schwab has produced a Noise analysis of the CLEAN algorithm in the case of
least squares minimization of a noiseless image which involves an
plane of the visibility data. Schwab has produced a Noise analysis of the CLEAN algorithm in the case of
least squares minimization of a noiseless image which involves an ![]() Matrix. However, no Noise
analysis has been performed for a real image.
Matrix. However, no Noise
analysis has been performed for a real image.
Poor modulation of short spacings results in an underestimation of the flux, which is manifested in a bowl of negative
surface brightness surrounding an object. Providing an estimate of the ``zero spacing'' flux (the total flux of the source,
which cannot be directly measured by an interferometer) can considerably reduce this
effect. Modulations or stripes can occur at spatial frequencies corresponding to undersampled parts of the ![]() plane.
This can result in a golf ball-like mottling for disk sources such as planets, or a corrugated pattern of parallel lines of
peaks and troughs (``stripes''). A more accurate model can be used to suppress the ``golf ball'' modulations, but may not
eliminate the corrugations. A tapering function which de-emphasizes data near
plane.
This can result in a golf ball-like mottling for disk sources such as planets, or a corrugated pattern of parallel lines of
peaks and troughs (``stripes''). A more accurate model can be used to suppress the ``golf ball'' modulations, but may not
eliminate the corrugations. A tapering function which de-emphasizes data near ![]() can also be used. Stripes
can sometimes be eliminated using the Cornwell smoothness-stabilized CLEAN (a.k.a. Prussian helmet algorithm; Thompson et al.
1986). CLEANing part way, then restarting the CLEAN also seems to eliminate the stripes, although this fact is more
disturbing than reassuring. Stability the CLEAN algorithm is discussed by Tan (1986).
can also be used. Stripes
can sometimes be eliminated using the Cornwell smoothness-stabilized CLEAN (a.k.a. Prussian helmet algorithm; Thompson et al.
1986). CLEANing part way, then restarting the CLEAN also seems to eliminate the stripes, although this fact is more
disturbing than reassuring. Stability the CLEAN algorithm is discussed by Tan (1986).
In order to CLEAN a map of a given dimension, it is necessary to have a beam pattern twice as large so a point source can be subtracted from any point in the map. Because the CLEAN algorithm uses a Fast Fourier Transform, the size must also be a Power of 2.
There are many variants of the basic Högbom CLEAN which extend the method to achieve greater speed and produce more realistic maps. Alternate nonlinear Deconvolution methods, such as the Maximum Entropy Method, may also be used, but are generally slower than the CLEAN technique. The Astronomical Image Processing Software (AIPS) of the National Radio Astronomical Observatory includes 2-D Deconvolution algorithms in the tasks DCONV and UVMAP. Among the variants of the basic Högbom CLEAN are Clark, Cornwell smoothness stabilized (Prussian helmet), Cotton-Schwab, Gerchberg-Saxton (Fienup), Steer, Steer-Dewdney-Ito, and van Cittert iteration.
In the Clark (1980) modification, CLEAN picks out only the largest residual points, and subtracts approximate point source
responses in the ![]() plane during minor (Högbom CLEAN) cycles. It only occasionally (during major cycles)
computes the full
plane during minor (Högbom CLEAN) cycles. It only occasionally (during major cycles)
computes the full ![]() residual map by subtracting the identified point source responses in the
residual map by subtracting the identified point source responses in the ![]() plane using a
Fast Fourier Transform for the Convolution. The Algorithm then returns to a minor cycle. This
algorithm modifies the Högbom method to take advantage of the array processor (although it also works without one). It
is therefore a factor of 2-10 faster than the simple Högbom routine. It is implemented as the AIPS task APCLN.
plane using a
Fast Fourier Transform for the Convolution. The Algorithm then returns to a minor cycle. This
algorithm modifies the Högbom method to take advantage of the array processor (although it also works without one). It
is therefore a factor of 2-10 faster than the simple Högbom routine. It is implemented as the AIPS task APCLN.
The Cornwell smoothness stabilized variant was developed because, when dealing with two-dimensional extended structures,
CLEAN can produce artifacts in the form of low-level high frequency stripes running through the brighter structure. These
stripes derive from poor interpolations into unsampled or poorly sampled regions of the ![]() plane. When dealing with
quasi-one-dimensional sources (i.e., jets), the artifacts resemble knots (which may not be so readily recognized as spurious).
APCLN can invoke a modification of CLEAN that is intended to bias it toward generating smoother solutions to the
deconvolution problem while preserving the requirement that the transform of the CLEAN components list fits the data. The
mechanism for introducing this bias is the addition to the Dirty Beam of a Delta Function (or ``spike'') of
small amplitude (PHAT) while searching for the CLEAN components. The beam used for the deconvolution
resembles the helmet worn by German military officers in World War I, hence the name ``Prussian helmet'' CLEAN.
plane. When dealing with
quasi-one-dimensional sources (i.e., jets), the artifacts resemble knots (which may not be so readily recognized as spurious).
APCLN can invoke a modification of CLEAN that is intended to bias it toward generating smoother solutions to the
deconvolution problem while preserving the requirement that the transform of the CLEAN components list fits the data. The
mechanism for introducing this bias is the addition to the Dirty Beam of a Delta Function (or ``spike'') of
small amplitude (PHAT) while searching for the CLEAN components. The beam used for the deconvolution
resembles the helmet worn by German military officers in World War I, hence the name ``Prussian helmet'' CLEAN.
The theory underlying the Cornwell smoothness stabilized algorithm is given by Cornwell (1982, 1983), where it is described
as the smoothness stabilized CLEAN. It is implemented in the AIPS tasks APCLN and MX. The spike performs a
Negative feedback into the dirty image, thus suppressing features not required by the data. Spike heights of a few
percent and lower than usual loop gains are usually needed. Also according to the MX documentation,
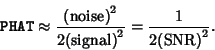
The Cotton-Schwab uses the Clark method, but the major cycle subtractions of CLEAN components are performed on ungridded
visibility data. The Cotton-Schwab technique is often faster than the Clark variant. It is also capable of
including the ![]() baseline term, thus removing distortions from noncoplanar baselines. It is often faster than the Clark
method. The Cotton-Schwab technique is implemented as the AIPS task MX.
baseline term, thus removing distortions from noncoplanar baselines. It is often faster than the Clark
method. The Cotton-Schwab technique is implemented as the AIPS task MX.
The Gerchberg-Saxton variant, also called the Fienup variant, is a technique originally introduced for solving the phase problem in electron microscopy. It was subsequently adapted for visibility amplitude measurements only. A Gerchberg-Saxton map is constrained to be Nonzero, and positive. Data and image plane constraints are imposed alternately while transforming to and from the image plane. If the boxes to CLEAN are chosen to surround the source snugly, then the algorithm will converge faster and will have more chance of finding a unique image. The algorithm is slow, but should be comparable to the Clark technique (APCLN) if the map contains many picture elements. However, the resolution is data dependent and varies across the map. It is implemented as the AIPS task APGS (Pearson 1984).
The Steer variant is a modification of the Clark variant (Cornwell 1982). It is slow, but should be
comparable to the Clark algorithm if the map contains many picture elements. The algorithm used in the program is due to
David Steer. The principle is similar to Barry Clark's CLEAN except that in the minor cycle only points above the (trim
level)![]() (peak in the residual map) are selected. In the major cycle these are removed using a Fast Fourier
Transform. If boxes are chosen to surround the source snugly, then the algorithm will converge faster and will have more
chance of finding a unique image. It is implemented in AIPS as the experimental program STEER and as the Steer-Dewdney-Ito
variant combined with the Clark algorithm as SDCLN.
(peak in the residual map) are selected. In the major cycle these are removed using a Fast Fourier
Transform. If boxes are chosen to surround the source snugly, then the algorithm will converge faster and will have more
chance of finding a unique image. It is implemented in AIPS as the experimental program STEER and as the Steer-Dewdney-Ito
variant combined with the Clark algorithm as SDCLN.
The Steer-Dewdney-Ito variant is similar to the Clark variant, but the components are taken as all pixels having residual flux greater than a cutoff value times the current peak residual. This method should avoid the ``ripples'' produced by the standard CLEAN on extended emission. The AIPS task SDCLN does an AP-based CLEAN of the Clark type, but differs from APCLN in that it offers the option to switch to the Steer-Dewdney-Ito method.
Finally, van Cittert iteration consists of two steps:
See also CLEAN Beam, CLEAN Map, Dirty Beam, Dirty Map
References
Christiansen, W. N. and Högbom, J. A. Radiotelescopes, 2nd ed. Cambridge, England: Cambridge University Press,
pp. 214-216, 1985.
Clark, B. G. ``An Efficient Implementation of the Algorithm `CLEAN'.'' Astron. Astrophys. 89, 377-378, 1980.
Cornwell, T. J. ``Can CLEAN be Improved?'' VLA Scientific Memorandum No. 141, 1982.
Cornwell, T. J. ``Image Restoration (and the CLEAN Technique).'' Lecture 9. NRAO VLA Workshop on Synthesis Mapping, p. 113, 1982.
Cornwell, T. J. ``A Method of Stabilizing the CLEAN Algorithm.'' Astron. Astrophys. 121, 281-285, 1983.
Cornwell, T. and Braun, R. ``Deconvolution.'' Ch. 8 in
Synthesis Imaging in Radio Astronomy: Third NRAO Summer School, 1988
(Ed. R. A. Perley, F. R. Schwab, and A. H. Bridle). San Francisco, CA: Astronomical Society of the Pacific, pp. 178-179, 1989.
Högbom, J. A. ``Aperture Synthesis with a Non-Regular Distribution of Interferometric Baselines.''
Astron. Astrophys. Supp. 15, 417-426, 1974.
National Radio Astronomical Observatory. Astronomical Image Processing Software
(AIPS) software package. APCLN, MX, and UVMAP tasks.
Pearson, T. J. and Readhead, A. C. S. ``Image Formation by Self-Calibration in Radio Astronomy.''
Ann. Rev. Astron. Astrophys. 22, 97-130, 1984.
Schwarz, U. J. ``Mathematical-Statistical Description of the Iterative Beam Removing Technique (Method CLEAN).'' Astron. Astrophys. 65, 345-356, 1978.
Tan, S. M. ``An Analysis of the Properties of CLEAN and Smoothness Stabilized CLEAN--Some Warnings.''
Mon. Not. Royal Astron. Soc. 220, 971-1001, 1986.
Thompson, A. R.; Moran, J. M.; and Swenson, G. W. Jr. Interferometry and Synthesis in Radio Astronomy.
New York: Wiley, p. 348, 1986.
|
|
|
© 1996-9 Eric W. Weisstein