|
|
|
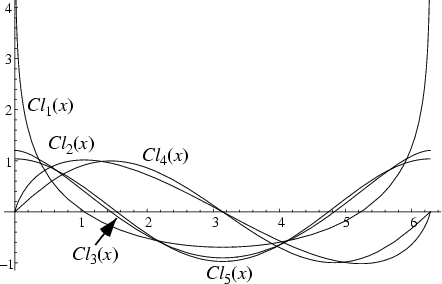
Define
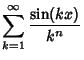 |
(1) | ||
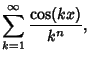 |
(2) |
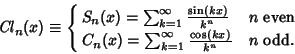 |
(3) |
| (4) |
| (5) |
The symbolic sums of opposite parity are summable symbolically, and the first few are given by
| (6) | |||
| (7) | |||
| (8) | |||
| (9) | |||
| (10) |
See also Clausen's Integral, Polygamma Function, Polylogarithm
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Clausen's Integral and Related Summations'' §27.8 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 1005-1006, 1972.
Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, p. 783, 1985.
Clausen, R. ``Über die Zerlegung reeller gebrochener Funktionen.'' J. reine angew. Math. 8, 298-300, 1832.
Grosjean, C. C. ``Formulae Concerning the Computation of the Clausen Integral
Jolley, L. B. W. Summation of Series. London: Chapman, 1925.
Wheelon, A. D. A Short Table of Summable Series. Report No. SM-14642. Santa Monica, CA: Douglas Aircraft Co., 1953.
![]() .''
J. Comput. Appl. Math. 11, 331-342, 1984.
.''
J. Comput. Appl. Math. 11, 331-342, 1984.
|
|
|
© 1996-9 Eric W. Weisstein