|
|
|
Gradshteyn and Ryzhik (1970) define circulants by
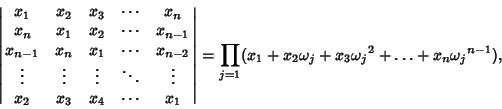 |
(1) |
| (2) |
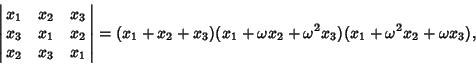 |
(3) |
The Eigenvalues ![]() of the corresponding
of the corresponding ![]() circulant matrix are
circulant matrix are
| (4) |
See also Circulant Matrix
References
Gradshteyn, I. S. and Ryzhik, I. M. Tables of Integrals, Series, and Products, 5th ed. San Diego, CA:
Academic Press, pp. 1111-1112, 1979.
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, p. 114, 1991.