A set of Orthogonal Polynomials defined as the solutions to the Chebyshev Differential Equation and denoted
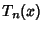 . They are used as an approximation to a Least Squares Fit, and are a special
case of the Ultraspherical Polynomial with
. They are used as an approximation to a Least Squares Fit, and are a special
case of the Ultraspherical Polynomial with 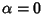 . The Chebyshev polynomials of the first kind
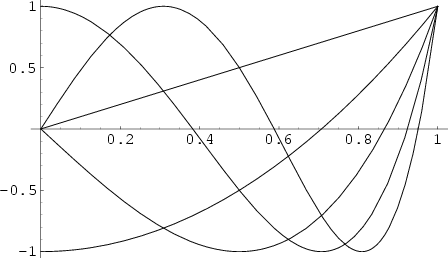
. The Chebyshev polynomials of the first kind 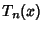 are
illustrated above for
are
illustrated above for ![$x\in[0,1]$](c1_1345.gif) and
and 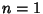 , 2, ..., 5.
, 2, ..., 5.
The Chebyshev polynomials of the first kind can be obtained from the generating functions
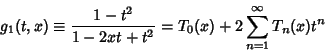 |
(1) |
and
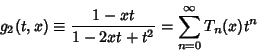 |
(2) |
for 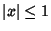 and
and 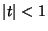 (Beeler et al. 1972, Item 15). (A closely related Generating Function is the basis
for the definition of Chebyshev Polynomial of the Second Kind.) They are normalized such that
(Beeler et al. 1972, Item 15). (A closely related Generating Function is the basis
for the definition of Chebyshev Polynomial of the Second Kind.) They are normalized such that 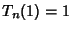 . They
can also be written
. They
can also be written
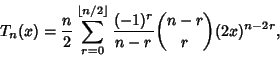 |
(3) |
or in terms of a Determinant
 |
(4) |
In closed form,
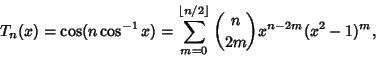 |
(5) |
where 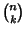 is a Binomial Coefficient and
is a Binomial Coefficient and
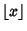 is the Floor Function.
Therefore, zeros occur when
is the Floor Function.
Therefore, zeros occur when
![\begin{displaymath}
x=\cos\left[{\pi (k-{\textstyle{1\over 2}})\over n}\right]
\end{displaymath}](c1_1354.gif) |
(6) |
for 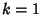 , 2, ...,
, 2, ..., 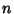 . Extrema occur for
. Extrema occur for
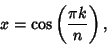 |
(7) |
where
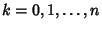 . At maximum,
. At maximum, 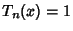 , and at minimum,
, and at minimum, 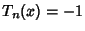 . The Chebyshev Polynomials are
Orthonormal with respect to the Weighting Function
. The Chebyshev Polynomials are
Orthonormal with respect to the Weighting Function
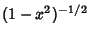
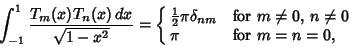 |
(8) |
where 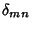 is the Kronecker Delta.
Chebyshev polynomials of the first kind satisfy the additional discrete identity
is the Kronecker Delta.
Chebyshev polynomials of the first kind satisfy the additional discrete identity
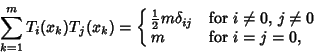 |
(9) |
where 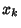 for
for 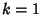 , ...,
, ..., 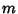 are the
are the 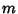 zeros of
zeros of 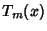 . They also satisfy the Recurrence
Relations
. They also satisfy the Recurrence
Relations
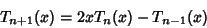 |
(10) |
![\begin{displaymath}
T_{n+1}(x)=xT_n(x)-\sqrt{(1-x^2)\{1-[T_n(x)]^2\}}
\end{displaymath}](c1_1366.gif) |
(11) |
for 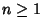 . They have a Complex integral representation
. They have a Complex integral representation
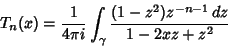 |
(12) |
and a Rodrigues representation
![\begin{displaymath}
T_n(x) = {(-1)^n\sqrt{\pi}\,(1-x^2)^{1/2}\over 2n(n-{\textstyle{1\over 2}})!} {d^n\over dx^n}[(1-x^2)^{n-1/2}].
\end{displaymath}](c1_1369.gif) |
(13) |
Using a Fast Fibonacci Transform with multiplication law
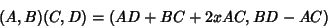 |
(14) |
gives
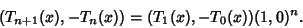 |
(15) |
Using Gram-Schmidt Orthonormalization in the range (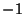 ,1) with Weighting Function
,1) with Weighting Function
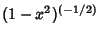 gives
gives
etc. Normalizing such that 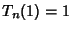 gives
gives
The Chebyshev polynomial of the first kind is related to the Bessel Function of the First Kind 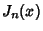 and
Modified Bessel Function of the First Kind
and
Modified Bessel Function of the First Kind 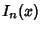 by the relations
by the relations
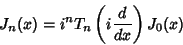 |
(19) |
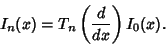 |
(20) |
Letting
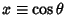 allows the Chebyshev polynomials of the first kind to be written as
allows the Chebyshev polynomials of the first kind to be written as
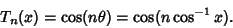 |
(21) |
The second linearly dependent solution to the transformed differential equation
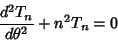 |
(22) |
is then given by
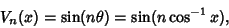 |
(23) |
which can also be written
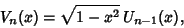 |
(24) |
where 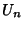 is a Chebyshev Polynomial of the Second Kind. Note that
is a Chebyshev Polynomial of the Second Kind. Note that 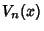 is therefore not a
Polynomial.
is therefore not a
Polynomial.
The Polynomial
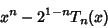 |
(25) |
(of degree 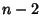 ) is the Polynomial of degree
) is the Polynomial of degree  which stays closest to
which stays closest to 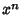 in the interval
in the interval 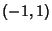 . The maximum
deviation is
. The maximum
deviation is 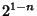 at the
at the 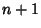 points where
points where
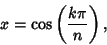 |
(26) |
for 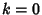 , 1, ...,
, 1, ..., 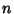 (Beeler et al. 1972, Item 15).
(Beeler et al. 1972, Item 15).
See also Chebyshev Approximation Formula, Chebyshev Polynomial of the Second Kind
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Orthogonal Polynomials.'' Ch. 22 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 771-802, 1972.
Arfken, G. ``Chebyshev (Tschebyscheff) Polynomials'' and ``Chebyshev Polynomials--Numerical Applications.''
§13.3 and 13.4 in
Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 731-748, 1985.
Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, Feb. 1972.
Iyanaga, S. and Kawada, Y. (Eds.). ``Cebysev (Tschebyscheff) Polynomials.'' Appendix A, Table 20.II in
Encyclopedic Dictionary of Mathematics. Cambridge, MA: MIT Press, pp. 1478-1479, 1980.
Rivlin, T. J. Chebyshev Polynomials. New York: Wiley, 1990.
Spanier, J. and Oldham, K. B. ``The Chebyshev Polynomials 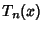 and
and 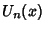 .''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
.''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() . They are used as an approximation to a Least Squares Fit, and are a special
case of the Ultraspherical Polynomial with
. They are used as an approximation to a Least Squares Fit, and are a special
case of the Ultraspherical Polynomial with ![]() . The Chebyshev polynomials of the first kind
. The Chebyshev polynomials of the first kind ![]() are
illustrated above for
are
illustrated above for ![]() and
and ![]() , 2, ..., 5.
, 2, ..., 5.
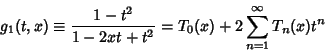
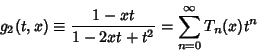
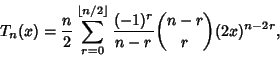

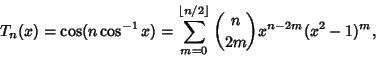
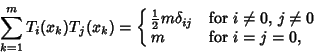
![]() ,1) with Weighting Function
,1) with Weighting Function
![]() gives
gives
![$\displaystyle \left[{x-{\int^1_{-1}x(1-x^2)^{-1/2}\,dx \over \int^1_{-1}(1-x^2)^{-1/2}\, dx}}\right]$](c1_1375.gif)
![$\displaystyle x-{[-(1-x^2)^{1/2}]^1_{-1}\over [\sin^{-1} x]^1_{-1}} = x$](c1_1376.gif)
![$\displaystyle \left[{x-{\int^1_{-1}x^3(1-x^2)^{-1/2}\,dx\over \int^1_{-1}x^2(1-x^2)^{-1/2}\,dx}}\right]x$](c1_1378.gif)
![$\displaystyle -\left[{\int^1_{-1}x^2(1-x^2)^{-1/2}\,dx\over \int^1_{-1}(1-x^2)^{-1/2}\,dx}\right]\cdot 1$](c1_1379.gif)
![$\displaystyle [x-0]x -{{\pi\over 2}\over \pi} = x^2-{\textstyle{1\over 2}},$](c1_1380.gif)
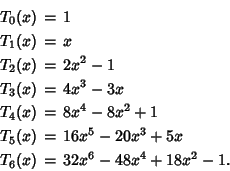
![]() and
Modified Bessel Function of the First Kind
and
Modified Bessel Function of the First Kind ![]() by the relations
by the relations
![]() allows the Chebyshev polynomials of the first kind to be written as
allows the Chebyshev polynomials of the first kind to be written as
![]() and
and ![]() .''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.
.''
Ch. 22 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 193-207, 1987.