|
|
|
A Catenary of Revolution. The catenoid and Plane are the only Surfaces
of Revolution which are also Minimal Surfaces. The catenoid can be given by
the parametric equations
| (1) | |||
| (2) | |||
| (3) |
| (4) | |||
| (5) | |||
| (6) |
| (7) |
| (8) | |||
| (9) |
| (10) |
| (11) |
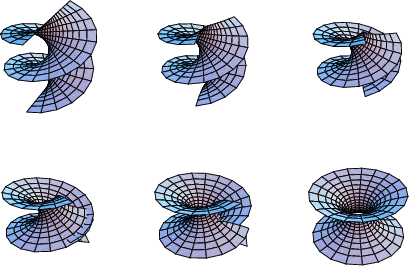
The Helicoid can be continuously deformed into a catenoid with ![]() by the transformation
by the transformation
| (12) | |||
| (13) | |||
| (14) |
See also Catenary, Costa Minimal Surface, Helicoid, Minimal Surface, Surface of Revolution
References
do Carmo, M. P. ``The Catenoid.'' §3.5A in
Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer).
Braunschweig, Germany: Vieweg, p. 43, 1986.
Fischer, G. (Ed.). Plate 90 in
Mathematische Modelle/Mathematical Models, Bildband/Photograph Volume.
Braunschweig, Germany: Vieweg, p. 86, 1986.
Geometry Center. ``The Catenoid.''
http://www.geom.umn.edu/zoo/diffgeom/surfspace/catenoid/.
Gray, A. ``The Catenoid.'' §18.4 Modern Differential Geometry of Curves and Surfaces.
Boca Raton, FL: CRC Press, pp. 367-369, 1993.
Meusnier, J. B. ``Mémoire sur la courbure des surfaces.'' Mém. des savans étrangers 10 (lu 1776), 477-510, 1785.
|
|
|
© 1996-9 Eric W. Weisstein