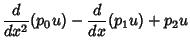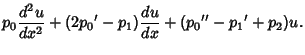Given a Second-Order Ordinary Differential Equation
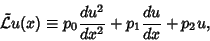 |
(1) |
where
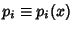 and
and 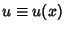 , the adjoint operator
, the adjoint operator
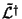 is defined by
is defined by
Write the two Linearly Independent solutions as 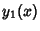 and
and 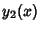 . Then the adjoint
operator can also be written
. Then the adjoint
operator can also be written
![\begin{displaymath}
{\tilde {\mathcal L}}^\dagger u = \int (y_2 {\tilde {\mathca...
...\,dx
= {\left[{{p_1\over p_0} ({y_1}'y_2-y_1{y_2}')}\right]}.
\end{displaymath}](a_389.gif) |
(3) |
See also Self-Adjoint Operator, Sturm-Liouville Theory
© 1996-9 Eric W. Weisstein
1999-05-25